Concept of Linear Convolution
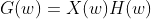
Convolution Properties
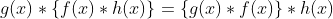
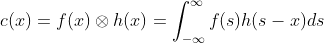
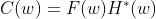
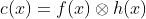
The concept of convolution is
central to Fourier theory and the analysis of Linear Systems. In fact the
convolution property is what really makes Fourier methods useful. In one
dimension the convolution between two functions, f (x) and h(x) is defined as:
Where ‘s’ is a dummy variable of
integration. This operation may be considered the area of overlap between the
function f(x) and the spatial (or time) reversed version of the function h(x). For
discrete signals the integration in above equation is replaced by summation. The result of the convolution of two simple
one dimensional functions is shown in figure 1.
The Convolution theorem relates
the convolution between the two real space (or time) domain signals to a multiplication in the
Fourier domain, and can be written as;
Convolution Properties
The convolution is a linear
operation which is distributive, so that for three functions f (x), g(x) and
h(x) we have that
If the two functions f (x) and
h(x) are of finite extent, (are zero outside a finite range of x), then the
extent (or width) of the convolution g(x) is given by the sum of the widths the
two functions. For example if figure 1 both f (x) and h(x) non-zero over the
finite range x = ±1. Thus the convolution g(x) is non-zero over the range x
= ±2.
If f[n] and h[n] are two finite length sequences of lengths L1 and L2
then g[n] will be of length L1+L2-1.
Correlation of two Signals
Correlation of two Signals
A closely related operation to
Convolution is the operation of Correlation of two functions. In Correlation
two functions are shifted and the area of overlap formed by integration, but
this time without the spatial (or time) reversal involved in convolution. The
Correlation between two function f (x) and h(x) is given by
This is for real signals, for
complex signals h*(s-x) is used, where h*(x) is the complex
conjugate of h(x). This operation is shown for two simple functions in figure 2.
If we compare the convolution in figure 1 and the correlation shown in figure 2,
the only difference is that the second function in correlation is not spatially
(or time) reversed and the direction of the shift is changed. Thus the correlation of two real functions f(t) and h(t), is equivalent to the convolution of f(-t) and h(t) or the convolution of f*(-t) (in case of complex functions) and h(t).
Figure 2: Correlation of two
simple functions.
The correlation is of more
importance, if we consider f (t) to be the signal and
h(t) to be the target” then we see that the correlation gives a peak
where the signal matches the target. This gives the
basis of the simple method of target detection. In the Fourier Domain the
Correlation Theorem becomes
The correlation is a linear
operation, which is distributive, but however is not commutative, since if
Autocorrelation
Autocorrelation is the cross-correlation
of a signal with itself. Informally, it is the
similarity between observations as a function of the time separation between
them. It is a mathematical tool for finding repeating patterns, such as the
presence of a periodic signal which has been buried under noise, or identifying
the missing fundamental frequency in a signal
implied by its harmonic
frequencies. It is often used in signal
processing for analyzing functions or series of values, such as time domain
signals.


No comments:
Post a Comment